Новые публикации: "Частота излучения фотона совпадает со средней частотой излучения электрона в переходе." >>>

Шидловский  Александр  Игнатьевич

кандидат  технических  наук

ATOM  ВОДОРОДА  – САМЫЙ  ПРОСТОЙ  ИЗ  АТОМОВ

Продолжение  теории  Нильса  Бора

На этом сайте продолжена теория атома водорода Бора, но не на языке квантовой механики, а на основе классической физики.

Простота используемой математики и ясность в изложении достигнуты благодаря введению нами двух допущений – постулатов:

1. Переход электрона между стационарными орбитами происходит согласно механике по спирально уменьшающимся орбитам.

2. В переходе электрон теряет энергию согласно электродинамике, испуская излучение фотона.

В нашей работе рассмотрены задачи, постановка которых до сих пор невозможна в квантовой механике.

Более подробно с материалом можно ознакомится в разделах данного сайта, полностью материал изложен в опубликованных книгах.

Разделы сайта:

Раздел 1.  Излучательный переход электрона в атоме
водорода Бора
1.1 Потеря энергии в переходе
1.2 Потеря момента количества движения
1.3 Время перехода электрона
1.4 Общие результаты

Раздел 2.  Переходы электрона с потерей орбитального
 момента в линиях серии Бальмера
2.1 Потеря энергии в переходах  4d2p,  5d2p, … nd2p
2.2 Потеря момента количества движения
2.3 Общие результаты   

Раздел 3.  Угловые моменты электрона
3.1 Противоречие старой квантовой теории
3.2 Орбитальный угловой момент
3.3 Общие результаты

Раздел 4.  Переходы электрона с ростом орбитального 
момента в линиях серии Бальмера
4.1 Потеря энергии в переходах 3s2p,  4s2p, 5s2p, … ns2p
4.2 Рост момента количества движения
4.3 Образование спектральной линии: классическое рассмотрение,
квантомеханический подход
4.4 Общие результаты

Раздел 5.  Частота излучения фотона совпадает со средней
частотой излучения электрона в переходе
5.1 Cредняя  частота  излучения  электрона для  круговых  орбит в переходе
5.1.1 Движение электрона в переходе
5.1.2 Удельная амплитуда волны излучения электрона
5.1.3 Средняя частота излучения электрона
5.2 Средняя частота излучения электрона для эллиптических орбит. Серия Лаймана
5.3 Средняя частота излучения электрона для эллиптических орбит. Серия Бальмера
5.4 Действие при движении  электрона по  стационарной   орбите
5.5 Гипотетическая серия

Введение

Очерк развития микрофизики

Направление исследования

ОЧЕРК  РАЗВИТИЯ  МИКРОФИЗИКИ

1.  АТОМНО – МОЛЕКУЛЯРНАЯ  ТЕОРИЯ

Согласно атомно-молекулярной теории все тела состоят из атомов. Более двух сотен лет ее развивали Бойль, Дантон, Лавуазье, Ломоносов, Гей-Люссак, Авогадро, Джоуль, Клаузиус, Максвелл, Лошмидт, Больцман, Гельмгольц и другие выдающиеся ученые … .

Все это время атомы оставались ненаблюдаемыми величинами. Свойства атомов изучались не в прямых, а в косвенных измерениях. Это измерения, результат которых определяют на основании прямых измерений других величин, но связанных с изучаемой величиной известной зависимостью.

В 1908 - 1910 годах после работ Эйнштейна, Смолуховского, Перрена, Резерфорда и других атомы перешли в разряд практически наблюдаемых величин, т.к. часть их характеристик стала наблюдаться в прямых измерениях, а характеристики, полученные в косвенных измерениях, прошли огромную научную и прикладную апробацию.

2.   ATOM   РЕЗЕРФОРДА

За начало развития микрофизики примем 1910 год, когда Резерфорд начал работу по определению размера и заряда ядра. Резерфорд обобщил результаты группы своих сотрудников и предложил ядерную модель строения атома, в которой он достаточно точно оценил размер и заряд ядра. Определяя размер и заряд ядра, Резерфорд использовал косвенные измерения. В их основе лежало измерение отклонения альфа частиц при их прохождении через тонкие металлические листочки.

Результаты анализа отклонения альфа частиц с применением методики косвенных измерений были апробированы много раз в других исследованиях, т.е. результаты Резерфорда по косвенному определению размера и заряда ядра прошли массовую научную и прикладную апробацию.

Таким образом, примерно за три года исследований Резерфорд сделал ядро атома практически наблюдаемой величиной в отношении его размера и заряда, как если бы эти величины были определены в прямых измерениях.

3. ATOM БОРА – ЗОММЕРФЕЛЬДА

1.   По теории атома водорода Бора, созданной в основном в 1913-1915 годах при использовании ядерной модели Резерфорда, электрон в атоме водорода вращается вокруг ядра по круговым стационарным орбитам. Каждая такая орбита характеризуется точными значениями радиуса , скорости , орбитального момента

вращающегося по ней электрона. При этом

ħ –  постоянная Планка,  

n – номер круговой стационарной орбиты или энергетического  состояния, а также главное квантовое число.

Величины _{, ,}  не прошли массовой научной и прикладной апробации, поэтому они отнесены к ненаблюдаемым величинам. Энергия электрона на n-ой круговой стационарной орбите определяется выражением

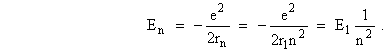
е  –   заряд электрона,

,   эВ  –  радиус и энергия электрона на первой,  круговой  стационарной орбите.

Энергия    стационарного состояния электрона и длина волны  λ  излучения фотона, вычисляемые в теории Бора, определяются в прямых измерениях, поэтому они отнесены к наблюдаемым величинам.

2.  Зоммерфельд продолжил в 1916 – 1918 годах теорию Бора.  Он рассмотрел эллиптические стационарные орбиты электрона. Используя координаты в плоскости орбиты: радиус вектор r и азимутальный угол φ, Зоммерфельд получил квантовые числа   и  .  Их сумма равна главному квантовому числу  n  теории Бора. Возможные значения азимутального квантового числа Зоммерфельда     определяются для стационарных орбит условием

Зоммерфельд уточнил выражение орбитального момента электрона для стационарных эллиптических (и круговых) орбит

Полуоси стационарных эллиптических орбит (большая   и   малая  ), скорость   электрона  и его орбитальный момент   вычисляются посредством косвенных измерений.

Эти величины не прошли массовой апробации, поэтому они отнесены к ненаблюдаемым величинам. Энергия   стационарного состояния электрона и длина волны λ излучения фотона, вычисляемые уточненной теорией Зоммерфельда, определяются в прямых измерениях и относятся к наблюдаемым величинам.

4.  РАБОТЫ  ЛАНДЕ.   КРИЗИС  В  МИКРОФИЗИКЕ

В 1919 – 1924 годах исследования в атомной физике сместились к изучению тонкой структуры спектральных линий и эффекта Зеемана.

В эти исследования большой вклад внес Ланде наряду с Зоммерфельдом и другими учеными. В 1919 году Ланде перенес в теорию атома векторное описание моментов импульса по аналогии с классической механикой. Было принято, что вектор момента атомного остова складывается с моментом импульса внешнего электрона. Это даёт вектор полного момента импульса атома. Но векторная модель встретилась с серьезной трудностью.

В результате анализа экспериментальных данных спектроскопии Ланде и другие исследователи пришли к выводу: вопреки векторной модели для энергетических s уровней орбитальное квантовое число  составляет не единицу, как это было в векторной модели, a ноль; т.е   для  p  уровней    ,  для d уровней      и  т.д.   Связь орбитального квантового числа  ,  с азимутальным квантовым числом Зоммерфельда дается соотношением

В 1923 году «полностью эмпирически» [4.1],  за два года до возникновения квантовой механики Ланде находит выражение для углового (орбитального) момента электрона

Определение величины   проводится в прямых измерениях, что позволяет отнести ее к наблюдаемым величинам. Расхождение в значениях пар величин ,      теории Бора – Зоммерфельда  и  ,     Ланде отмечено историком квантовой физики Джеммером: «Старая квантовая теория так и не смогла разрешить это противоречие» [4.2].   Примерно с 1920 года в атомной физике начинает утрачиваться представление о строении даже простейшего атома водорода. Считается, что к этому времени старая квантовая теория «...представляла собой ...скопление гипотез, принципов, теорем и вычислительных рецептов...»   Под старой квантовой теорией понимаются результаты, полученные в атомной физике до 1925 года, когда начала развиваться квантовая механика  [4.3].  В целом, такое состояние было названо кризисом в физике.

4.1)   Биденхарн Л.,  Лаук Дж.   Угловой момент  в квантовой физике.   

                                                                   Т. 2. М.: Мир, 1984. С. 317.

4.2)   Джеммер М.    Эволюция понятий квантовой механики.

М.: Наука, 1985. С. 134.

4.3)   Джеммер М.    Эволюция понятий квантовой механики.

                                                   М.: Наука, 1985. С. 196.

5.   ПОСТРОЕНИЕ   КВАНТОВОЙ   МЕХАНИКИ 

НА    ОСНОВЕ   НАБЛЮДАЕМЫХ   ВЕЛИЧИН

1.  К 1925 году состояние микрофизики было сложным, в частности,  из-за расхождения теории атома водорода Бора – Зоммерфельда с экспериментальными данными, полученными при изучении тонкой структуры спектральных линий и эффекта Зеемана.

Каждую теоретическую задачу микрофизики надо было решать на языке классической физики, а затем решения переводить на квантовый язык, придерживаясь принципа соответствия Бора. Такой перевод часто был делом догадки и интуиции.

В истории развития физики кризисы в понимании природы происходили многократно. Преодолевались они медленным, «распутыванием» неясных мест и привлечением новых экспериментальных данных. В этом процессе участвовали наблюдаемые и ненаблюдаемые величины.

2.  Зимой 1925 года 23-летний Гейзенберг начал работать в Институте Бора в Копенгагене. «С большой пользой для себя я постоянно следил за тем, как Бор развивал физическое толкование формул; я же предпочитал использовать формальный математический принцип ...» и здесь же Гейзенберг продолжает: «... я, презирая всякие наглядные картины, использовал свою формальную точку зрения на поставленную им проблему...»  [5.1].   Отметим здесь следующее. Предпочтение «формального математического принципа» и «презрение ко всяким наглядным картинам» характеризует Гейзенберга скорее как математика, чем физика.

Летом 1925 года Гейзенберг обобщил дискуссии с Бором и изложил свои мысли о новой, квантовой механике. Бор заинтересовался этой работой «... и уже не имел возражений против «радикального отказа от наглядных картин...»  [5.2]. Бор так писал об этом в 1925 году: «В теории Гейзенберга делается попытка ..., чтобы на каждой стадии вычислений входили только величины, доступные непосредственному наблюдению» [5.3], т.е. в основу квантовой механики включаются только наблюдаемые величины.

В сложной обстановке, сложившейся в атомной физике к 1925 году, Гейзенберг посчитал рациональным при построении квантовой механики стать на формальную точку зрения. Он включил в теорию только наблюдаемые величины, стараясь избежать ошибок, обусловленных наглядными, но возможно нереальными моделями.

3.  Это не бесспорно. Более 300 лет Физика в своем развитии включала в теорию ненаблюдаемые величины, которые экспериментальной проверкой «сортировались» на  наблюдаемые  и  ложные. Теория, пополнившись найденными наблюдаемыми величинами, вводила в свой объем новые ненаблюдаемые величины. Процесс «сортировки» практикой повторялся. Таким образом, теория развивалась методом проб и ошибок.

Гейзенберг, включив в квантовую механику только наблюдаемые величины, сумел зафиксировать существующее состояние микрофизики, но заложил основание квантовой теории с пониженным потенциалом развития.

4.  В связи с «обеднением» материала для построения квантовой механики (из-за отказа от ненаблюдаемых величин) Гейзенберг, по-видимому, вынужден был использовать мощный математический аппарат, основу которого составляли матрицы. Гейзенберг не был специалистом матричного исчисления, также как и его прежний руководитель,   Борн, который  обратился к математикам: Иордану, Винеру, Гильберту.  Они с его помощью завершили матричный вариант квантовой механики, оказавшийся настолько сложным, что не мог адекватно восприниматься большинством физиков.

В качестве наблюдаемых в квантовой механике Гейзенберг использовал энергию стационарного состояния , частоту, интенсивность излучения спектральных линий, угловой момент электрона   Ланде. При этом как бы отпала необходимость рассматривать противоречие старой квантовой теории, поскольку в квантовую механику вошла пара величин    и    ,  а ненаблюдаемая пара  и   оказалась вне рассмотрения.

Таким образом, на начальном этапе микрофизики Гейзенберг свернул с трехсотлетнего пути развития физики, где в теории сосуществовали как наблюдаемые, так и ненаблюдаемые величины.

Шредингер в 1926 году развил волновой вариант квантовой механики, который основывался на тех же наблюдаемых величинах, что и матричный вариант. Используя только наблюдаемые величины, Шредингер продолжил движение Гейзенберга, отличное от обычного пути физики.

В том же 1926 году Дирак закрепил это направление Гейзенберга, создав теорию представлений, из которой матричная и волновая механика следовали как некоторые виды абстрактной алгебры.

5.  В соответствии с принципом своего построения квантовая механика не описывает движение частицы в пространстве и во времени. В отличие от классической механики, где можно указать одновременно значения механических величин: импульса, момента импульса, координат, энергии частицы, в квантовой механике можно указать лишь средние величин и вероятности их появления значения  [5.4].

Таким образом, в квантовой механике движение описывается статистически. «Это вполне соответствует тому, что квантовая механика есть по существу теория статистическая...»  [5.5–6].

6.  Квантовая механика завершила свое принципиальное формирование примерно к 1929 году. В дальнейшем плодотворно развивались её практические приложения в атомной технике, химии, физике твердого тела, электронике, оптике, и в других отраслях, что обусловлено способностью квантовой механики, указать средние значения величин и  вероятность  их появления.

7.  Квантовая механика позволяет многое рассчитать в области микрофизических процессов, однако с ее помощью трудно понять само физическое явление. Приведем высказывание нобелевского лауреата за 1965 год Фейнмана: «…мне кажется, я смело могу сказать, что квантовой механики никто не понимает. ... Если сможете, не мучайте себя вопросом: Но как же так может быть?  Ибо в противном случае вы зайдете в тупик, из которого еще никто не выбирался»  [5.7].

Приведем взгляд профессора Мухина. Когда он знакомился с квантовой механикой, то был поражен, услышав слова профессора: «...понять квантовую механику невозможно, к ней можно только привыкнуть»  [5.8].

Эту «непонятность» иллюстрирует Ферми, нобелевский лауреат за 1938 год. Он был на семинаре, где обсуждалась его теория бета-распада. «Я уже не могу уследить за высоконаучными теориями учеников Оппенгеймера. На их семинаре я был подавлен своей неспособностью, понять их», - говорит Ферми близкому другу Сегре, - «Утешила меня только последняя фраза: «В этом и состоит фермиевская теория бета-распада»   [5.9].

Читатель сам ощутит эту «непонятность» квантовой механики, например, из описания прохождения фотонов через поляризаторы: «... каждый фотон, хотя и является неделимым квантом излучения, тем не менее, проходя между призмами Николя, должен все же «каким-то образом» расщепляться на две компоненты, которые затем вновь соединяются второй призмой Николя»  [5.10].

Здесь, видимо, квантовая механика соприкасается с такими сторонами микрофизики, которые не описываются существующей теорией.

  5.1)    Нильс Бор.   Жизнь и творчество.     Сб. Статей.

             Составитель  Франкфурт У.И.        М.: Наука, 1967. С. 6.

  5.2)    Нильс Бор.   Жизнь и творчество.    Сб. Статей.

             Составитель Франкфурт У.И.       М.: Наука, 1967. С. 9-10.

  5.3)    Нильс  Бор.    Избранные научные труды.

                                       Т. 2. М.: Наука, 1971.  С. 22.

  5.4)    Соколов А.А.,  Тернов И. М.,  Жуковский В. Ч.  Квантовая механика.  

                                М.: Наука, 1979. С. 88.

  5.5)    Шпольский Э. В.    Атомная физика. Т. 2.

                                                М.: Наука, 1984.  С. 60-61.

  5.6)    Блохинцев Д. И.   Основы квантовой механики.

                                                    М.: Наука, 1983.  С. 12-13.

  5.7)    Фейнман Р.   Характер физических законов.

                                            М.: Наука, 1987.  С. 117.

  5.8)    Мухин К.   Занимательная ядерная физика.

                                  М.: Атомиздат. 1969.  С. 75.

  5.9)    Сегре Э.     Энрико Ферми.   Физик.

                                 М.: Мир, 1973.  С. 178-179.

5.10)   Липкин Г.   Квантовая механика.

                          Перевод с англ.  М.: Мир, 1977.  С. 38.

6. НАПРАВЛЕНИЕ ИССЛЕДОВАНИЯ

1.  В своей основополагающей работе Бор пишет в 1913 году: «Динамическое равновесие системы в стационарных состояниях можно рассматривать с помощью обычной механики, тогда как переход системы из одного стационарного состояния в другое нельзя трактовать на этой основе» [6.1].

Таким образом, по мысли Бора,  процесс перехода  электрона между стационарными орбитами (состояниями)  нельзя  рассматривать на  основе  механики.

2.  Примерно в начале 1924 года Дирак … «впервые узнал о боровских орбитах»,  и  он  активно изучал их:  «Большая проблема  состояла в том, каким образом различные боровские орбиты в атоме  взаимодействуют друг с другом.  …  Однако, эта работа оказалась по существу бесплодной и ни к чему не привела.

Внезапный перелом произошел в 1925 году, когда Гейзенберг ввел свою матричную механику … .  Мне в то время потребовалось много усилий,  для того чтобы отказаться от боровских орбит»  [6.2]. 

Можно видеть, что Дирак первоначально глубоко изучал «боровские орбиты» и, кроме того, пытался рассмотреть их «взаимодействие друг с другом», т.е. рассмотреть  переход  электрона между  стационарными орбитами.

Однако, после введения Гейзенбергом абстрактного, матричного подхода к теории атома Дирак «отказался от боровских орбит», хотя до того он был  «их сильным приверженцем».

3.   Вскоре после работы Гейзенберга появилась работа  Шредингера, где он предпочел нейтральную математическую форму: «Не стоит даже упоминать насколько приятнее будет нам представление, что энергия при квантовом переходе переходит из одной формы колебаний в другую, чем представление о прыгающих электронах »      [6.3].

Таким образом, мысль Бора о неприменимости  «обычной механики»  к рассмотрению перехода электрона между стационарными орбитами была закреплена последующими работами Гейзенберга, Шредингера, а затем и Дирака.

4.  Это положение сохраняется в квантовой теории: «Теория Бора была наглядна в том, что касалось стационарных состояний … .  Зато основной для физики атома процесс излучения … был лишен такой наглядности. Что означает скачок электрона с одной дозволенной орбиты на другую, … как представить течение этого процесса во времени?  Электронным скачкам было трудно подыскать какую-либо аналогию в классической физике» [6.4].

Таким образом,  возможность построения классической картины перехода электрона между стационарными орбитами (состояниями) остаётся   не  исследованной.

5. Отсутствие  таких исследований, а также исторический опыт включения в теорию ненаблюдаемых величин обусловили нашу попытку продолжить теорию атома водорода Бора - Зоммерфельда («параллельно» квантомеханическому подходу) с того состояния, когда она была оставлена авторами примерно к 1925 году. Наша попытка возвращает микрофизику на обычный путь развития физики, где в теории сосуществуют как наблюдаемые, так и ненаблюдаемые величины.

 Особенность нашего подхода заключается в том, что мы предположили для атома водорода:

5.1. Переход электрона происходит по спирально  уменьшающимся эллиптическим (или круговым) орбитам согласно обычной механике.

5.2. В переходе электрон постепенно теряет энергию с интенсивностью согласно электродинамике, испуская излучение фотона.

Эта наглядная модель дала возможность применить для описания перехода электрона сравнительно простой  аппарат классической физики.

В нашей работе в качестве актуального направления теории атома водорода рассмотрен процесс излучательного перехода электрона между стационарными орбитами. Здесь использованы те же ненаблюдаемые величины, что и в теории Бора - Зоммерфельда:  радиусы и полуоси стационарных орбит, орбитальный момент электрона Зоммерфельда. Эти ненаблюдаемые величины в случае научной и прикладной апробации могут стать практически наблюдаемыми, как это было с «ненаблюдаемыми» атомами в атомно-молекулярной теории и определением размера и заряда ядра Резерфордом.

Реализуя попытку продолжить теорию атома водорода Бора - Зоммерфельда, нами опубликованы пять частей работы  (пять Книг).

В первой части рассмотрены переходы электрона 2p1s, 3d2p, 4f 3d, ... между соседними круговыми стационарными орбитами. Эти и другие переходы показаны на Рисунке 1.6.1. Здесь в переходе орбитальный момент электрона уменьшается  [6.5].

По оси ординат слева дана энергия Е электрона в электрон-вольт (эВ).

По оси ординат справа дано «относительное» значение энергии электрона:

По оси абсцисс (показана сверху) приведены значения азимутального квантового числа    Зоммерфельда и орбитального квантового числа   Ланде.

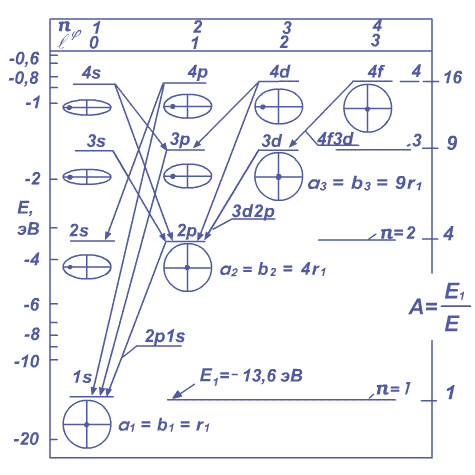
      Рисунок 1.6.1.    Упрощенная схема энергетических уровней и  излучательных переходов электрона  в атоме водорода.     Эллиптические и   круговые орбиты электрона показаны иллюстративно, ядро дано в виде точки.   Большие полуоси эллиптических орбит условно даны    одного размера.

Во второй книге рассмотрены переходы электрона 4d2p, 5d2p, 6d2p между эллиптическими стационарными орбитами и второй круговой стационарной орбитой [6.6]. Эти переходы обусловливают образование линий серии Бальмера. В переходе орбитальный момент электрона также уменьшается.

В третьей книге рассмотрены угловые моменты электрона: орбитальный, полный и спиновый. Показана связь этих моментов с орбитальным моментом электрона Зоммерфельда  [6.7].

В четвертой книге  рассмотрены переходы электрона 3s2p, 4s2p, 5s2p , ... между эллиптическими стационарными орбитами и второй круговой стационарной орбитой, обусловливающие образование линий серии Бальмера. Здесь в переходе орбитальный момент электрона увеличивается. Сопоставлены классический и квантомеханический подходы к образованию спектральной линии   [6.8].

В пятой книге для линий серии Лаймана и Бальмера определена средняя частота излучения энергии электроном в течение перехода. Эта средняя частота оказалась равной частоте излучения фотона данного перехода. Определена величина действие в форме Лагранжа, Мопертюи и Гамильтона для движения электрона по стационарным орбитам.

В целом, в нашей работе на основе классической физики рассматриваются задачи, постановка которых обычно невозможна в квантовой механике из-за ее специфической «замкнутости», что обусловлено, видимо фактором отсутствия ненаблюдаемых величин. «... Заключив себя в рамки квантовой механики, мы построили себе дом без окон и дверей, что ...не очень понятно, дом это или тюрьма»,  –   таково мнение нобелевского лауреата по физике за 1978 г.    Салама А.  [6.9].

В работе используется система СГС (гауссова система единиц), поскольку для области квантовой физики система единиц СИ достаточно «... неудобна» [6.10].      В ряде работ отмечается целесообразность использования системы единиц     СГС в этой области.

Мы благодарим за критический просмотр содержания первой, второй и третьей части нашей работы к.ф.-м.н. Егорова O.K., .,   к.ф.-м.н. Дитлова В.А.,    д.ф.-м.н. Преснякова Л.П.,  которые дали стимулирующие рецензии и отзыв.

Данное   Введение может привлечь внимание работающих в области атомной физики, исследователей, студентов, а также заинтересованных читателей.

6.1)     Нильс Бор.   Избранные научные труды.       Т. 1. 

                     М.: Наука, 1970.  С.  90;  аналогичные представления  С. 1 95, 250.

6.2)     Поль  Дирак.    Собрание научных трудов.  Т.4. 

                                           М.:  Физматлит,  2005.  С.  679-680.

6.3)     Шредингер Э. Квантование как задача о собственных  значениях.

                                      Первое сообщение.  Ann. d. Phys.,  1926,  Bd. 79,  4,  s. 375.

6.4)     Л.С.  Полак.    Сб. статей:  50 лет квантовой механики. 

                                                                        М.:  Наука,  1979.  С.  58.

6.5)     Шидловский А.И.    Атом водорода - самый простой из атомов.

                                                       Минск: ВЭВЭР, 1997. С. 47-127.

6.6)     Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                   Часть вторая.        М.: УРСС, 1998. С. 13-78.

6.7)     Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                  Часть третья.       М.: Вестник, 2000. С. 13-63.

6.8)     Шидловский А.И.   Атом водорода - самый простой из атомов. 

                                                   Часть четвертая.    M.  BИCMA,  2002. С. 17-77.

6.9)     Салам А.   Успехи физических наук.

                                      1969. Т. 99. В. 4. С. 573

6.10)   Шпольский Э.В.  Атомная физика.  Т. 1.

                                                    М.: Наука, 1984. С. 9.

Подробнее с материалом можно ознакомится в разделах данного сайта, полностью материал изложен в опубликованных книгах.