Шидловский  Александр  Игнатьевич

кандидат  технических  наук

ATOM  ВОДОРОДА – САМЫЙ  ПРОСТОЙ  ИЗ  АТОМОВ

Продолжение  теории  Нильса  Бора 

Книга  5

5.   ЧАСТОТА  ИЗЛУЧЕНИЯ  ФОТОНА

СОВПАДАЕТ  СО СРЕДНЕЙ  ЧАСТОТОЙ  ИЗЛУЧЕНИЯ

ЭЛЕКТРОНА  В  ПЕРЕХОДЕ

(Представленный материал соответсвует главе 9 книги 5 )

Теория атома водорода, развиваемая автором, возвращает логику и механику в границы конкретной научной модели. Оказалось, что переход электрона между стационарными орбитами можно описать классическими формулами, причем результаты хорошо совпадают с квантовыми формулами и с эмпирическими данными. Дальнейшие исследования в этом направлении могут иметь стратегическое значение для «водородной энергетики», которая идет на смену «углеводородному топливу».

5.1 Cредняя  частота  излучения  электрона для  круговых  орбит   в  переходе

5.1.1   Движение электрона в переходе
5.1.2  Удельная амплитуда волны излучения электрона
5.1.3   Средняя частота излучения электрона
Обзор глав: 10, 11, 12, 13  книги 5

Рассмотрен наиболее простой случай движения электрона в переходе по круговым, спирально уменьшающимся орбитам. В параграфах  5.1.1÷ 5.1.3  показано, что средняя частота, излучаемая электроном в переходе, равна частоте фотона, испущенного в этом переходе.

5.1.1   ДВИЖЕНИЕ  ЭЛЕКТРОНА  В  ПЕРЕХОДЕ

1.  Рассмотрим переходы электрона между соседними,  круговыми стационарными орбитами в атоме водорода.

Это переходы  2p1s,  3d2p,  4f3d  и т.д.  Они показаны на Рисунке  9.2.1, где по оси ординат слева дана энергия Е  электрона в электрон-вольт (эВ).

По оси ординат справа дано «относительное» значение энергии электрона

  –  энергия электрона на первой, круговой стационарной орбите, в 1s состоянии,

,  E  –   стационарное и текущее значение энергии электрона  в переходе,

A   –   относительное значение большой полуоси   а  орбиты,

b  –   малая полуось орбиты электрона,

   –   радиус первой,  круговой стационарной орбиты,

n   –   стационарное (целое) и текущее значение главного квантового

          числа в переходе.

По оси абсцисс (показана сверху) приведены значения азиму­тального квантового числа    Зоммерфельда и орбитального кван­тового числа  ℓ  Ланде.

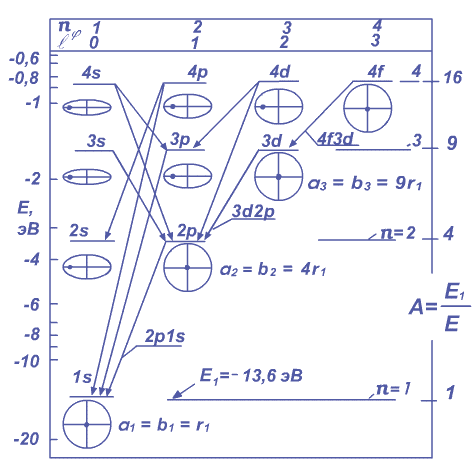
Рисунок   9.2.1.  Схема энергетических уровней и излучательных переходов в  атоме водорода  Бора – Зоммерфельда.  Иллюстративно показаны эллиптические и круговые орбиты электрона  вокруг ядра.   Большие полуоси орбит даны  условно одного размера.

2.  В процессе перехода между соседними, круговыми стационарными орбитами электрон движется по круговым, спирально уменьшающимся орбитам с текущим радиусом r. Определяя среднюю частоту излучения, испускаемого электроном в течение перехода, будем  обращаться  к  2p1s переходу, дающего первую линию серии Лаймана  (Рисунок 9.2.1).

Частота   обращения электрона вокруг ядра в  переходе   возрастает по мере уменьшения относительного радиуса  R  орбиты и по мере уменьшения главного квантового числа n   [ 9.2.1 ]:

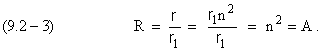
  –   частота обращения электрона вокруг ядра  по первой, круговой

            стационарной орбите в атоме водорода,

  –   частота излучения  энергии электроном в переходе,

            согласно электродинамике,  увеличивается соответственно

            росту текущей частоты обращения  электрона  :

Так в начале 2p1s перехода, при  ,  текущая частота обращения  и  излучения

  ,

а в конце перехода ( )  эти частоты  в  восемь раз выше:

Интенсивность  J  излучения  электрона на текущей  круговой  орбите [ 9.2.2 ]

с учетом  (9.2-3):

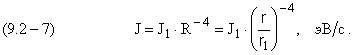
 –  интенсивность излучения, которую согласно электродинамике должен  испускать   электрон на первой,  круговой стационарной орбите   в атоме  водорода.

Двигаясь в переходе по круговым,  спирально уменьшающимся орбитам, электрон испускает текущую частоту излучения    с  нарастающей  интенсивностью,  т.к.  n  и  R   уменьшаются.

9.2.1)    Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                    Минск: ВЭВЭР, 1997. С. 32.

9.2.2)    Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                    Минск: ВЭВЭР, 1997. С. 90.

5.1.2  УДЕЛЬНАЯ  АМПЛИТУДА  ВОЛНЫ  ИЗЛУЧЕНИЯ ЭЛЕКТРОНА

При усреднении частот складываются амплитуды G  волн излучения, а не их интенсивности  J.  Амплитуда  волны связана с  интенсивностью   квадратичной зависимостью [ 9.3.1 ].

На  n-ой круговой стационарной орбите  амплитуда волны с учетом (9.2-7):

, .    

При движении электрона вокруг ядра характерным временем  является период  обращения  и  равный ему  период   излучения энергии электроном. 

 –  период обращения электрона вокруг ядра по первой,

                                           круговой стационарной орбите [ 9.3.2 ].

Для круговой,  n-ой стационарной орбиты запишем выражение удельной амплитуды волны, которая излучается в течение  периода  обращения  :

 –  удельная амплитуда волны излучения, которую согласно электродинамике,

          должен испускать электрон на первой,  круговой стационарной орбите

          в течение  периода  обращения  .

Величина  g  имеет размерность действия в степени 0,5.  Она  характеризует частость («интенсивность»)  излучения частоты ,  определяемой по (9.2-4), в течение периода Т.

В процессе перехода электрона между n-ой и (n –1)-ой  круговыми стационарными  орбитами удельная амплитуда волны излучения с учетом (9.3-3)  и  (9.2-3):

Отношение удельных амплитуд на  (n –1)-ой  и более дальней  соседней n-ой круговой стационарной орбите

Наибольшее значение (9.3-5), равное двум, соответствует 2p1s переходу, а для  перехода  , например, оно снижается до  .

Таким образом, удельная амплитуда волны излучения  g  сравнительно слабо изменяется в течение перехода электрона между соседними  круговыми  стационарными орбитами.

9.3.1)    Бутиков  Е.И.     Оптика. 

                                         М.: Высшая школа, 1986. С. 32.

9.3.2)    Шидловский А.И.  Атом водорода - самый простой из атомов.

                                                    Минск: ВЭВЭР, 1997. С. 32.

9.3.3)    Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                    Минск: ВЭВЭР, 1997. С. 90.

9.3.4)    Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                    Минск: ВЭВЭР, 1997. С. 105.

9.3.5)    Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                    Минск: ВЭВЭР, 1997. С.16-17.  С. 105.

5.1.3   СРЕДНЯЯ  ЧАСТОТА   ИЗЛУЧЕНИЯ ЭЛЕКТРОНА

1.  В течение перехода между n-ой и (n –1)-ой  соседними круговыми стационарными орбитами частота  излучения электрона по (9.2-4)  имеет непрерывное распределение своих значений от    до .

Для определения  средней  частоты  применим выражение теории вероятностей

[ 9.4.1 ]

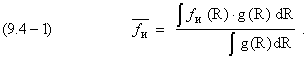
Здесь в числителе  –  сумма произведений текущей частоты излучения на её «вес» (частость), а в знаменателе сумма «весов» всех частот.

Подставляя в (9.4-1)      по (9.2-4)  и   g   по  (9.3-4),  определим среднюю частоту излучения электрона, испускаемую им в результате перехода между n-ой и (n –1)-ой круговыми стационарными орбитами:

   .    

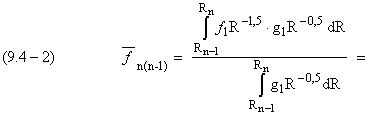
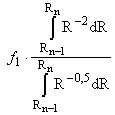Интегрируя  (9.4-2),  получим

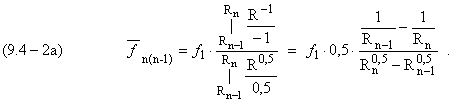
Для  круговой стационарной орбиты по  (9.2-3)

         .

Тогда  знаменатель  (9.4-2а)  упрощается

,

и  для  (9.4-2а)  получим

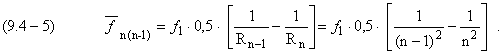
2.  Сопоставим выражение (9.4-5)  для средней  частоты  излучения  электрона в переходе с формулой Бора для частоты     излучения  фотона этого перехода.

 В случае перехода электрона между  n-ой  и  (n–1)-ой  круговыми  стационарными орбитами  формула Бора дает для частоты излучения фотона  [ 9.4.2 ]:

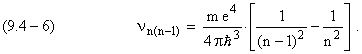
m,  e  –  масса и заряд электрона,  

  –  запись постоянной  Планка. 

Упростим  (9.4-6),  используя выражения теории Бора [ 9.4.3 ]:

 –  скорость электрона на первой, круговой стационарной орбите с радиусом .

Подставим в   (9.4-6)  выражения  (9.4-7)  и   (9.4-8)

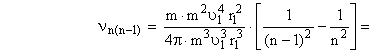
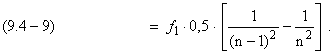
Таким образом, в случае перехода электрона по круговым, спирально уменьшающимся орбитам выражение  (9.4-5)  для  средней частоты излучения электрона совпадает с формулой Бора для частоты излучения фотона, полученной им в 1913 году на основе использования закона сохранения энергии.

Выражение (9.4-5)  для  средней частоты    излучения

электрона получено здесь с помощью представления  о вращении электрона вокруг ядра в переходе по круговым  спирально уменьшающимся орбитам и использования среднего  значения теории вероятностей.

Для   2p1s  перехода можно записать с учетом  (9.4-5):

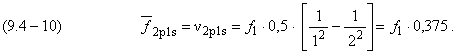
Следовательно,  дан  частично  ответ на вопрос Лоренца о механизме образования света «согласно теории Бора».  Показано, что в случае перехода электрона  между соседними  круговыми стационарными орбитами его средняя  частота  излучения в переходе совпадает с  частотой   излучения фотона этого перехода.

9.4.1)    Шпольский Э.В.   Атомная физика. 

                                         Т.1. М.: Наука, 1984. С. 534.

9.4.2)    Собельман  И.И.   Введение в теорию атомных спектров.

                                                      М.: Наука, 1977.  С. 15.

9.4.3)   Шидловский А.И.   Атом водорода - самый простой из атомов.

                                                    Минск: ВЭВЭР, 1997. С. 16, 21.

ОБЗОР  ГЛАВ   10, 11, 12, 13   КНИГИ  5

В Главах  девятой, десятой и одиннадцатой книги 5 сделана попытка в решении вопроса, поставленного в 1923 году нобелевским лауреатом Лоренцем: «…в конце концов как образуется свет согласно теории Бора». [ 5.1 ].

Рассмотрены переходы, приводящие к образованию линий серии Лаймана и Бальмера.  Переходы электрона происходят между стационарными орбитами.

В течение перехода электрон движется вокруг ядра по круговым или эллиптическим, спирально уменьшающимся орбитам.

Используется наглядная модель движения электрона и применяется простая математика.

1.  Введена  удельная  амплитуда  волны  излучения,  характеризующая излучение электрона в течение периода обращения его по орбите.

2.  Определено средствами классической физики  среднее  расстояние  электрона от ядра на эллиптической орбите.  Оно оказалось близким по аналитическому выражению к среднему расстоянию, найденному квантовой  механикой.

3.  Оценено  число оборотов  электрона вокруг ядра в переходе и  время перехода  электрона.

4.  Время перехода электрона сопоставлено со временем жизни перехода по данным квантовой механики. В целом, получена корреляция значений сопоставляемых величин, хотя физический смысл их несколько различен.

5.  Для спектральных линий серии Лаймана и Бальмера определена средняя частота излучения энергии электроном в течение  перехода, которая оказалась  равной  частоте излучения фотона этого перехода. В этом случае дается, по-видимому, частичный ответ на вопрос Лоренца.  Остается не ясным механизм «концентрирования» излучения электрона в течение перехода в  направленное излучение фотона.

Остается по-прежнему неясным причина отсутствия дипольного излучения электрона в стационарных состояниях (на стационарных орбитах).

В Главе  двенадцатой  рассмотрена важная величина  –   действие  применительно к  стационарным  орбитам электрона.

1.   Используя орбитальные характеристики при движении электрона по стационарным орбитам, определено  действие  в форме Лагранжа,  Мопертюи  и  Гамильтона.

2.  Вычислены составляющие действия,  определяемые переносной и радиальной скоростью электрона для стационарных орбит.  Эти составляющие в теории Бора – Зоммерфельда были постулированы.

3.   Согласно механике, полученное  постоянное  значение действия для электрона на стационарной орбите указывает, по-видимому, что это движение является  фактическим, среди других  кинематически  возможных  движений.       

В Главе  тринадцатой  (в порядке обсуждения)  рассмотрена гипотетическая серия линий, обусловленная переходами электрона с  ns  уровней на протон  р  ядра атома водорода. В качестве примера рассмотрен гипотетический  2sp  переход.

Наша работа может привлечь внимание специалистов атомной физики, исследователей, студентов, заинтересованных читателей.

5.1)    Джеммер  М.   Эволюция понятий квантовой механики.

                                                  М.: Наука, 1985.  С. 158.

Наша работа может привлечь внимание специалистов атомной физики, исследователей, студентов, заинтересованных читателей.

Подробно данный материал изложен в книге: 

Шидловский А.И.    Атом водорода - самый простой из атомов.  Книга  5.

Продолжение теории Нильса Бора.  М.: Издательство ЛКИ , 2007. – 144 С.

Цена книги 90 рублей.

Использование материалов сайта допускается только с письменного разрешения автора.