
Новые публикации: "Частота излучения фотона совпадает со средней частотой излучения электрона в переходе." >>>
Шидловский Александр Игнатьевич
ATOM ВОДОРОДА – САМЫЙ ПРОСТОЙ ИЗ АТОМОВ
Продолжение теории Нильса Бора
Книга 4
4. ПЕРЕХОДЫ ЭЛЕКТРОНА С РОСТОМ
ОРБИТАЛЬНОГО МОМЕНТА В ЛИНИЯХ
СЕРИИ БАЛЬМЕРА
Представлена интернет-версия (сокращенный вариант) Книги 4
4.1
Потеря энергии в переходах 3s2p, 4s2p, 5s2p, … ns2p
4.2
Рост момента количества движения
4.3
Образование спектральной линии: классическое рассмотрение,
квантомеханический подход
4.4
Общие результаты
Рассмотрены переходы, приводящие к образованию линий серии Бальмера. Здесь излучательные переходы электрона происходят между стационарными эллиптическими и круговой орбитами. В течение перехода электрон движется вокруг ядра по эллиптическим, спирально уменьшающимся орбитам, а его орбитальный момент увеличивается на постоянную Планка ħ.
4.1. ПОТЕРЯ ЭНЕРГИИ В ПЕРЕХОДЕ
В этой части нашей работы рассмотрены переходы: 3s2p, 4s2p, 5s2p, … ns2p. [4.1.1].
Они показаны на Рисунке 4.1.1, где по оси ординат слева дана энергия Е электрона в электрон-вольт (эВ). По оси ординат справа дано «относительное» значение энергии электрона:
![]()
n – номер круговой стационарной орбиты или энергетического
состояния электрона, а также главное квантовое число,
![]() – большая
полуось текущей эллиптической орбиты.
– большая
полуось текущей эллиптической орбиты.
По оси абсцисс (дана сверху) приведены
значения азимутального квантового числа ![]() Зоммерфельда и орбитального
квантового числа ℓ Ланде.
Зоммерфельда и орбитального
квантового числа ℓ Ланде.
В n-ом энергетическом состоянии (на n-ой стационарной эллиптической орбите) электрон обладает энергией
.
![]()
![]() – относительное значение большой полуоси
эллиптической
– относительное значение большой полуоси
эллиптической
стационарной орбиты
![]()
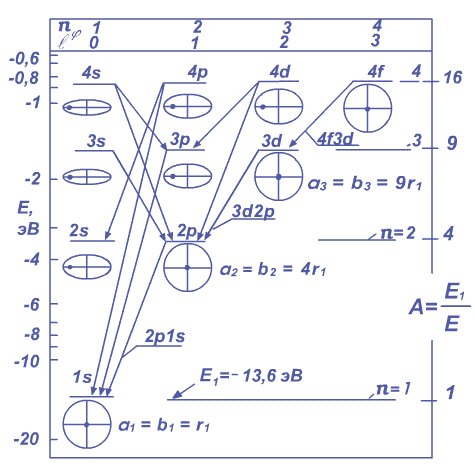
Рисунок 4.1.1. Упрощенная схема энергетических уровней и излучательных переходов электрона в атоме водорода. Эллиптические и круговые орбиты электрона показаны иллюстративно, ядро дано в виде точки. Большие полуоси эллиптических орбит условно даны одного размера.
Покажем процесс постепенной потери энергии электроном в ns2p переходе [4.1.2]. Отнесем выражение (4.1 – 2) к текущему энергетическому состоянию электрона в течение перехода
![]()
![]() –
относительное значение большой полуоси текущей
–
относительное значение большой полуоси текущей
эллиптической орбиты.
Дифференцируя (4.1 – 4), получим потерю энергии dE электроном при уменьшении относительного значения большой полуоси на dA:
![]()
Интегрируя (4.1–5) с учетом (4.1–2), получим количество энергии, постепенно теряемое электроном в ns2p переходе и уносимое с излучением фотона, здесь n ≥ 3 :
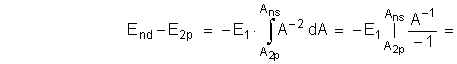
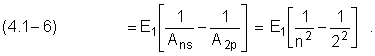
Количество энергии, теряемое электроном в процессе перехода, совпадает с полученным на основе закона сохранения энергии.
Теперь процесс перехода предстает как постепенная потеря энергии электроном в зависимости от уменьшения относительного значения большой полуоси эллиптической орбиты А или от уменьшения главного квантового числа n.
4.1.1) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть 4. М.: ВИСМА, 2002. С. 14-79.
4.1.2) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть 4. М.: ВИСМА, 2002. С. 22-24.
4.2. РОСТ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
Рассмотрим изменение момента количества движения электроном в ns2p переходе.
Запишем выражение для текущего момента количества движения электрона, вращающегося вокруг ядра по эллиптической орбите [4.2.1]:
![]()
b, E – текущие значения малой полуоси эллиптической орбиты и энергии
электрона (по абсолютной величине) в процессе перехода,
m – масса электрона.
Перепишем (2.2–1), используя (2.1–2)
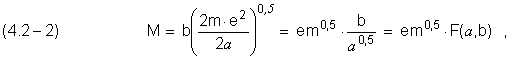
т.е. текущий момент количества движения
электрона является функцией двух переменных: F( ![]() , b).
, b).
Запишем (4.2–2) с учетом (4.1–1)
и выражения теории Бора
![]() [4.2.2] :
[4.2.2] :
![]()
![]()
В – относительная величина малой полуоси эллиптической орбиты
электрона.
![]()
Следовательно:
![]()
Таким
образом, текущее значение азимутального квантового числа
![]() равно отношению относительных значений
малой полуоси В
и большой полуоси А в степени одна вторая. С другой стороны,
текущее значение
равно отношению относительных значений
малой полуоси В
и большой полуоси А в степени одна вторая. С другой стороны,
текущее значение ![]() равняется
относительному значению момента количества движения электрона.
равняется
относительному значению момента количества движения электрона.
Определим, аналогично [4.2.3], потерю момента количества движения электроном в 3s2p переходе, который обусловливает образование первой линии серии Бальмера [4.2.4].
Запишем полный дифференциал функции
F( ![]() , b) выражения (4.2–2):
, b) выражения (4.2–2):
![]()
Интегрируя (2.2.–6), получим потерю момента количества движения электроном в переходе:
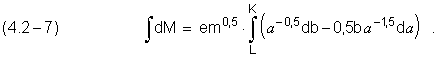
К, L – точки начала и конца перехода (или начальный и конечный энергетические уровни).
На Рисунке 2.2.1 нанесена
начальная точка ![]() и конечная точка
и конечная точка ![]() ,
между которыми проходит «траектория» 3s2p перехода электрона.
,
между которыми проходит «траектория» 3s2p перехода электрона.
По оси ординат (справа) даны относительные значения малой полуоси В, а по оси абсцисс даны относительные значения большой полуоси А в степени одна вторая.
Значение момента количества движения, теряемого электроном в переходе, не зависит от вида «траектории» [4.2.5] .
В качестве «траектории» изменения переменных А0,5 и В принята прямая линия, которая нанесена на Рисунке 4.2.1 между точками К и L.
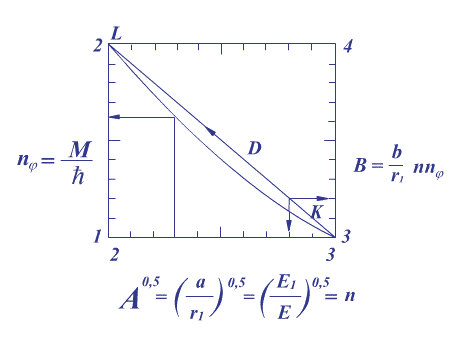
Рисунок 4.2-1. Изменение относительных значений полуосей
( В
и ![]() )
текущей эллиптической орбиты электрона в процессе 3s2p перехода.
)
текущей эллиптической орбиты электрона в процессе 3s2p перехода.
Параметры точек К, D и L прямой линии возьмем из Таблицы 4.2.1.
Таблица 4.2.1.
| Обозначение точки |
Параметры точки (переход 3s2p) |
| K (начальная) |
|
| D (промежуточная) |
|
| L (конечная) |
|
Запишем «траекторию» изменения переменных А0,5 и В в течение 3s2p перехода как уравнение прямой линии, показанной на Рисунке 4.2.1.
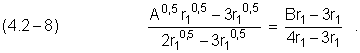
Упростим (4.2 – 8):
![]()
![]()
Используя (4.2–9), (4.2–4) и (4.1–1) запишем:
![]()
![]()
Подставим эти значения в (4.2 – 7) и получим:
![]()
![]()
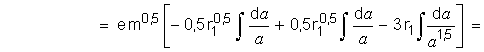
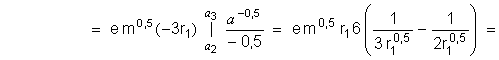
Напомним:
![]()
![]() и
и ![]() .
.
Потеря момента количества движения в 3s2p переходе составит:
![]() .
.
Отрицательное значение потери орбитального момента электрона равносильно его увеличению в результате 3s2p перехода.
Таким образом, момент количества движения, постепенно приобретаемый электроном в процессе 3s2p перехода, оказывается равным постоянной Планка ħ.
Важное значение результата (4.2–13) состоит в том, что постоянная Планка ħ получает простой физический смысл. Она равна интегралу (сумме) приростов текущего момента количества движения электрона в процессе его 3s2p перехода по спирально уменьшающимся эллиптическим орбитам.
Отметим следующее. Момент количества движения, приобретаемый электроном, выражается через постоянную Планка ħ. Это указывает на возможность применения классической физики для описания явлений микромира.
Описание процесса роста момента количества движения электроном в ns2p переходе несколько трудоемко. Однако все преобразования доступны студенту технического института.
4.2.1) Ландау Л. Д., Лившиц Е.М. Механика.
М.: Наука, 1965. С. 8.
4.2.2) Шидловский А.И. Атом водорода – самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 16.
4.2.3) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть вторая. М.: УРСС, 1998. С. 27.
4.2.4) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть четвертая. М.: ВИСМА, 2002. С. 24-32.
4.2.5) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть вторая. М.: УРСС, 1998. С. 29.
4.3.
ОБРАЗОВАНИЕ СПЕКТРАЛЬНОЙ ЛИНИИ
Классическое рассмотрение
1. Согласно классической физике, оптике, акустике и радиотехнике образование спектральной линии основывается на рассмотрении волновых цугов, испущенных при колебаниях электрона осциллятора или электрона атома или испущенных радиотехническим устройством.
Классическая физика рассматривает электрон в атоме как «вибратор», излучающий электромагнитные волны. В качестве модели используется осциллятор. Это положительный заряд большой массы и отрицательный легкий заряд (электрон), могущий совершать около него колебания.
В случае «внешнего толчка» электрон осциллятора переходит в определенное возбужденное состояние и начинает колебаться, постепенно сбрасывая энергию возбуждения в виде волн, называемых волновым цугом.
Используя теорию Максвелла, классическая физика дает выражение для убывающей энергии E колеблющегося электрона [4.3.1] :
![]()
![]() – начальное значение энергии колебаний электрона.
– начальное значение энергии колебаний электрона.
![]() – время
«жизни» возбужденного состояния
электрона осциллятора
– время
«жизни» возбужденного состояния
электрона осциллятора
или длительность сигнала радиотехнического устройства;
в целом, это время испускания энергии излучения в виде
волнового цуга.
2. При попадании единичного волнового цуга на вход идеального спектрального прибора (с аппаратной шириной
![]() )
на выходе формируется спектр
цуга с шириной [4.3.2]:
)
на выходе формируется спектр
цуга с шириной [4.3.2]:
![]()
Таким образом, спектральная ширина ![]() единичного
цуга излучения определяется длительностью
единичного
цуга излучения определяется длительностью ![]() цуга,
т.е. длительностью испускания энергии.
цуга,
т.е. длительностью испускания энергии.
3. Регистрация излучения волновых цугов идеальным спектральным прибором обусловливает на выходе образование спектральной линии с такой же шириной, что и спектр единичного цуга [4.3.3] :
![]()
Величину ![]() называют естественной шириной спектральной линии. Она не зависит от числа зарегистрированных волновых цугов.
называют естественной шириной спектральной линии. Она не зависит от числа зарегистрированных волновых цугов.
Таким образом, длительность времени «жизни» ![]() возбужденного
состояния электрона осциллятора
или длительность сигнала
возбужденного
состояния электрона осциллятора
или длительность сигнала ![]() радиоустройства связаны с естественной шириной спектральной
линии
радиоустройства связаны с естественной шириной спектральной
линии ![]() известным
соотношением [4.3.4]:
известным
соотношением [4.3.4]:
![]()
которое можно охарактеризовать и так: «… Произведение продолжительности обрывка синусоиды на ширину его спектра есть величина постоянная» [4.3.5].
В оптике, акустике и радиотехнике выражение (4.3 – 4) – основа для проектирования и массового применения приборов.
Выражение (4.3 – 4)
прошло практическую апробацию, его составляющие ![]() и
и ![]() являются наблюдаемыми величинами в акустике, радиотехнике и часто в оптике, если
позволяют экспериментальные возможности наблюдения.
являются наблюдаемыми величинами в акустике, радиотехнике и часто в оптике, если
позволяют экспериментальные возможности наблюдения.
4. Сделаем обобщение.
В классической физике, оптике, акустике и радиотехнике :
а) длительность сигнала ![]() определяется временем испускания энергии
электромагнитного излучения;
определяется временем испускания энергии
электромагнитного излучения;
б) естественная ширина спектральной линии ![]() определяется длительностью сигнала
определяется длительностью сигнала
![]() через выражение (4.3
– 4);
через выражение (4.3
– 4);
В нашей работе выполняются оба пункта этого обобщения.
5. В нашей работы [4.3.6] определено, например, время перехода электрона между 2p и 1s основным (нижнем) состоянием:
![]()
В течение времени 2p1s перехода по круговым, спирально уменьшающимся орбитам электрон непрерывно излучает энергию с интенсивностью согласно электродинамике.
Эта энергия (в виде «обрывка синусоиды») уносится с фотоном, временная продолжительность которого приравнена к времени 2p1s перехода электрона:
![]()
Таким образом, временная продолжительность фотона
![]() определяется длительностью
определяется длительностью ![]() испускания
энергии электроном в 2p1s переходе.
Это реализует пункт а)
Обобщения 4.
испускания
энергии электроном в 2p1s переходе.
Это реализует пункт а)
Обобщения 4.
6. Частота излучения
фотона, определяемая формулой Бора
[4.3.7], для случая ![]() :
:
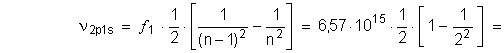
![]()
![]() – частота
обращения электрона по первой круговой стационарной орбите [4.3.8] .
– частота
обращения электрона по первой круговой стационарной орбите [4.3.8] .
Таким образом, на вход спектрометра поступают фотоны с частотой ![]() , частотный спектр каждого
из них, с учетом (4.3 – 4), составит:
, частотный спектр каждого
из них, с учетом (4.3 – 4), составит:
![]()
При регистрации фотонов на выходе идеального спектрометра по (4.3 – 3) образуется спектральная линия с той же (естественной) шириной
![]() Это реализует пункт б)
Обобщения 4.
Это реализует пункт б)
Обобщения 4.
На Рисунке 4.3.1. в виде спектральной линии дан частотный спектр фотонов испущенных в результате 2p1s перехода. Такой же спектр образуется на выходе идеального спектрометра. Этот рисунок иллюстрирует выражения (4.3 – 7) и (4.3 – 8).
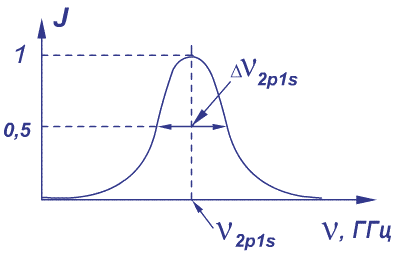
Рисунок 4.3.1. Спектральная линия – частотный спектр излучения фотонов, испущенных в результате 2p1s перехода электрона.
На выходе идеального спектрометра образуется спектральная линия с
той же (естественной) шириной ![]() .
.
По оси ординат: J – интенсивность огибающей частотного спектра,
в относительных единицах.
По оси абсцисс:
![]() – частота
излучения в ГГц ( 1 ГГц = 109 Гц ),
– частота
излучения в ГГц ( 1 ГГц = 109 Гц ),
![]() – частота излучения
фотона, испущенного в
– частота излучения
фотона, испущенного в
результате 2p1s перехода электрона.
![]() – ширина частотного
спектра излучения фотона,
– ширина частотного
спектра излучения фотона,
равная естественной ширине спектральной
линии.
Таким образом, в продолженной нами теории атома водорода Бора образование спектральной линии согласуется с классической физикой, оптикой, акустикой и радиотехникой.
4.3.1) Шпольский Э.В. Атомная физика.
Т. 1. М.: Наука, 1984. С. 226.
4.3.2) Бутиков Е.И. Оптика.
М.: Высшая школа, 1986. С.52.
4.3.3) Бутиков Е.И. Оптика.
М.: Высшая школа, 1986. С. 57.
4.3.4) Гоноровский И.С. Радиотехнические цепи и сигналы.
М.: Радио и связь, 1986. С. 45-48.
4.3.5) Горелик Г.С. Колебания и волны.
М.: Техтеориздат, 1950. С. 512.
4.3.6) Шидловский А.И. Атом водорода - самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 79.
4.3.7) Шидловский А.И. Атом водорода - самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 106.
4.3.8) Шидловский А.И. Атом водорода - самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 32.
КВАНТОМЕХАНИЧЕСКИЙ ПОДХОД
1. Квантомеханическое описание спектральной линии основано на работах Дирака, Вайскопфа, Вигнера, Гайтлера и других ученых.
Особенность здесь в образовании спектральной линии заключается в следующем.
Энергетические «... уровни атома принимаются не бесконечно резкими. Поэтому вследствие «размазывания» термов (уровней) переходу с одного терма на другой будет соответствовать нерезкая спектральная линия, и мы получим конечную ширину линии» [4.3.9].
Таким образом, согласно квантовой теории ширина спектральной линии обусловлена наличием широкого, «размазанного» возбужденного уровня атома.
2. В основе этого положения
лежит соотношение неопределенностей. Действительно: «... Размазанность термов (уровней) находит себе объяснение в соотношении неопределенности Гейзенберга между энергией и временем. Конечная продолжительность
жизни ![]() терма
вызывает неопределенность его энергии
порядка ∆Е ...» [4.3.9] или иначе
[4.3.10] :
терма
вызывает неопределенность его энергии
порядка ∆Е ...» [4.3.9] или иначе
[4.3.10] :
![]()
«Следовательно, ширина уровня определяется выражением
![]()
Основное состояние атома стационарно (из него невозможен спонтанный переход в другие состояния). Поэтому энергия основного состояния является определенной вполне точно. Вследствие конечной ширины возбужденных уровней энергия испускаемых атомами фотонов имеет разброс, описываемый в квантовой теории той же кривой, которая дана на Рисунке 4.31» [4.3.11] и которая заимствована у классической физики на основе «принципа соответствия» Бора.
![]() – среднее время «жизни» возбужденного
состояния. Это время, за которое число атомов, находящихся в данном возбужденном
состоянии уменьшается в
– среднее время «жизни» возбужденного
состояния. Это время, за которое число атомов, находящихся в данном возбужденном
состоянии уменьшается в
![]() [4.3.12] .
[4.3.12] .
Таким образом, согласно квантовой механике излученные широким возбужденным уровнем
фотоны имеют несколько различные энергии ![]()
в пределах разброса ![]() всего уровня.
всего уровня.
Для фотона энергии ![]() внутри разброса
внутри разброса
![]() энергий фотонов запишем
энергий фотонов запишем
![]()
![]() – частота излучения
фотона энергии
– частота излучения
фотона энергии
![]() .
.
Для получения выражения, связывающего ширину уровня по энергии с
шириной уровня по частоте, возьмем конечные интервалы в выражении
(4.3 –11):
![]()
т.е. фотоны, испущенные широким, возбужденным уровнем
![]() имеют несколько различные частоты излучения
имеют несколько различные частоты излучения
![]() в пределах разброса
в пределах разброса
уровня ![]() .
.
Таким образом, применяя «принцип соответствия», квантовая механика заимствует у классической физики, оптики, акустики, радиотехники так
называемую дисперсионную кривую (Рисунок 4.3.1), чтобы выразить распределение
фотонов по энергии (и по частоте) внутри «размазанного» уровня
шириной
![]() ( и
( и
![]() ).
).
Подставляя (4.3 – 12) в (4.3 – 9), получим
![]()
или
![]()
Выражение (4.3 – 13), даваемое квантовой механикой, сходно с выражением (4.3 – 4), полученным классической физикой, оптикой, акустикой, радиотехникой и ходом нашего рассмотрения по (4.3 – 8).
Выражение (4.3 – 13) связывает среднее время жизни ![]() электрона
на возбужденном уровне с шириной
электрона
на возбужденном уровне с шириной ![]() частот фотонов, испускаемых
частот фотонов, испускаемых
электроном в переходе;
![]() и
и
![]() ненаблюдаемые величины.
ненаблюдаемые величины.
Следовательно, согласно
квантовой механике на вход идеального спектрометра поступают фотоны несколько
различной частоты ![]() в пределах ширины
в пределах ширины ![]() .
.
На выходе такого спектрометра по квантовой теории образуется
спектральная линия шириной ![]() . Эта естественная ширина
. Эта естественная ширина ![]() линии просто «включает» в себя все фотоны частотой
линии просто «включает» в себя все фотоны частотой ![]() , испущенные «размазанным»
уровнем шириной
, испущенные «размазанным»
уровнем шириной
![]() .
.
Однако фактически спектральные
приборы работают иначе. Поступающий
на вход идеального спектрометра фотон (цуг излучения, «обрывок» синусоиды, импульс)
с временной продолжительностью
![]() преобразуется спектрометром При
этом на выходе дается соответственно спектральная огибающая фотона шириной
преобразуется спектрометром При
этом на выходе дается соответственно спектральная огибающая фотона шириной
![]() .
.
Поток фотонов, регистрируемых спектрометром, увеличивает «амплитуду» огибающей спектральной линии, но ее естественная ширина остается прежней:
![]()
Особенность квантовой механики в том, что она не определяет время перехода электрона и время испускания фотона [4.3.13]. Поэтому квантомеханический подход, видимо, не может использовать теорию спектральных приборов для описания механизма образования спектральной линии.
Косвенным указанием на трудности квантового описания спектральной линии является частое отсутствие этого материала в учебниках по квантовой механике [4.3.14] или дается его схематическое изложение [4.3.15].
4.3.9) Вайскопф В. Успехи физических наук – 1933, Т. 3.
В. 4, С. 577.
4.3.10) Гайтлер В. Квантовая теория излучения.
М.: ИЛ, 1956. С. 129.
4.3.11) Савельев И.В. Курс общей физики.
М.: Наука, 1987. С. 104.
4.3.12) Савельев И.В. Курс общей физики.
М.: Наука, 1987. С. 103.
4.3.13) Нильс Бор. Избранные научные труды.
Т. 1. М.: Наука, 1970. С. 530.
4.3.14) Блохинцев Д.И. Основы квантовой механики.
М.: Наука, 1983. 664 С.
4.3.15) Шпольский Э.В. Атомная физика.
Т. 1. М.: Наука, 1984. С. 400-401.
Приведем некоторые другие результаты, полученные нами в четвертой части нашей работы.
Для электрона в переходе по спирально уменьшающимся эллиптическим орбитам определены:
– переносная, радиальная и общая скорость;
– переносное, радиальное и общее ускорение;
– кинетическая, потенциальная и полная энергия;
– интенсивность излучения энергии;
– число оборотов электрона в переходе и время перехода.
Для рассмотренных ns2p переходов, приводящих к образованию линий серии Бальмера, полученные результаты согласуются с нашим предположением об эллиптическом характере движения электрона в переходе между стационарными эллиптическими и круговой орбитами в атоме водорода.
При этом используется наглядная модель движения электрона и применяется простая математика.
Наша работа может привлечь внимание специалистов атомной физики, исследователей, студентов, заинтересованных читателей.
Подробно данный материал изложен в книге
Шидловский А.И. Атом водорода - самый простой из атомов. Книга 4.
Продолжение теории Нильса
Бора М.: ВИСМА, 2002. 79 С.
Цена
книги 40 рублей.
Автор с признательностью примет замечания и предложения
по адресу: 127576, Москва, ул. Череповецкая, д. 14, кв. 168,
по телефону: 8(499) 200-94-28,
по эл. почте: E-mail:Shidlowsky@gmail.com
Шидловскому Александру Игнатьевичу.
По вопросу приобретения опубликованных книг можно обратиться по указанному здесь адресу.
Использование материалов сайта допускается только с письменного разрешения автора.