Шидловский А.И. Книга 3. Спектральные линии. Орбитальное квантовое число Ланде. Азимутальное число Зоммерфельда. Орбитальный, полный и спиновый моменты электрона. Векторные диаграммы. Анализа угловых моментов

Представлена интернет-версия (сокращенный вариант) Книги 3

В 1919 – 1924 годах исследования в атомной физике в значительной мере сместились к изучению тонкой структуры спектральных линий и эффекта Зеемана. Здесь уже имелся большой объем экспериментального материала. Бор и Зоммерфельд, создавая теорию атома водорода, изучали в основном процессы образования спектральных линий. После 1918 года большинство исследований стало проводиться по изучению отличий между компонентами спектральной линии. Эти процессы энергетически гораздо слабее, чем процессы, ответственные за образование спектральной линии и обусловленные переходом электрона между стационарными уровнями (стационарными орбитами).

В 1923 году, за два года до возникновения квантовой механики в результате анализа данных спектроскопии Ланде и другие ученые «чисто эмпирически» [3.1.1] пришли, в частности, к следующему.

Орбитальный угловой момент электрона дается формулой

которая отлична от выражения теории Бора – Зоммерфельда:

– орбитальное квантовое число, даваемое выражением

– азимутальное квантовое число, введенное Зоммерфельдом.

Применение выражений (3.1–1), и (3.1–3) наряду с выражениями для полного и спинового угловых моментов, также найденных в то время «полностью эмпирически» Ланде, позволило дать объяснение тонкой структуры спектров и многим деталям расщепления линий в магнитном поле (эффект Зеемана) в согласии с экспериментом.

В обоих случаях использования орбитальных квантовых чисел и Ланде и Зоммерфельд опирались в своих исследованиях на большие объемы, но разных экспериментальных данных.

Известный историк квантовой физики Джеммер так отметил это разногласие: «старая квантовая теория так и не смогла разрешить это противоречие» [3.1.2]. Под старой квантовой теорией понимаются результаты, полученные в атомной физике до 1925 года, когда начала развиваться квантовая механика.

Таким образом, примерно с 1923 года в атомной физике утрачивается наглядное представление о строении простейшего из атомов – атома водорода. Одной из причин этого является «неразрешенное противоречие» между значениями величин , теории Бора – Зоммерфельда и величин , , полученных эмпирически Ланде и использованных квантовой механикой.

Для решения вопроса нами сделано предположение: значения величин , , характеризующие орбитальный момент электрона теории Бора – Зоммерфельда не противоречат несколько другим значениям величин , , характеризующие орбитальный момент электрона, найденный эмпирически Ланде. Отсутствие противоречия объясняется тем, что каждая пара величин , и , описывают свою область физической реальности. Эти области разные, хотя и достаточно близкие. Иными словами и являются разными физическими характеристиками движения электрона.

В соответствии с этим предположением в данной, третьей части нашей работы [3.1.3] рассмотрены с применением классической физики угловые моменты электрона: орбитальный, полный и спиновый. В связи с новизной подхода полученные результаты оцениваются как первое приближение.

3.1.1) Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике.

3.1.2) Джеммер М. Эволюция понятий квантовой механики.

3.1.3) Шидловский А.И. Атом водорода – самый простой из атомов.

1. Рассмотрим орбитальный угловой момент электрона, введенный в атомную физику Ланде (воспринятый затем квантовой механикой) и момент количества движения электрона теории Бора – Зоммерфельда. В основу анализа положим данные, приведенные в Таблице 3.2.1.

В первой и четвертой строках Таблицы 3.2.1 приведены азимутальное квантовое число Зоммерфельда и орбитальное квантовое число Ланде (квантовой механики).

Во второй, третьей, а затем в пятой и шестой строках даны значения в первой степени и в квадрате, а также значения в первой степени и в квадрате.

№ пп	ПАРАМЕТР	Единица измерения	Значение параметра (абсолютное или относительное по отношению к или )
1.		–	1	2	3	4	10
2.			1	2	3	4	10
3.			1	4	9	16	100
4.		–	0	1	2	3	9
5.			0	± 1,41	± 2,45	± 3,46	± 9,49
6.			0	2	6	12	90
7.			1	2	3	4	10
8.		–	0	1	2	3	9
9.		–	– 1	– 2	– 3	– 4	– 10
10.			1	2	3	4	10
11.			–1	–2	–3	– 4	–10

В седьмой строке даётся разность квадратов моментов, обозначенная как :

Результат выражения (3.2-1) получен путем использования численных данных из третьей и шестой строк таблицы.

Здесь квадрат орбитального углового момента представлен как разность квадратов моментов.

Выражения (3.2–1), (3.2-2) указывают на связь орбитального углового момента Ланде (квантовой механики) с моментом количества движения электрона теории Бора – Зоммерфельда.

2. Запишем результат (3.2–2), т.е. параметр шестой строки таблицы 3.2.1, следующим образом

Корнями этого квадратного уравнения являются

Подставим численные значения из шестой строки в (3.2-4) и в (3.2-5), получим

Первый корень уравнения (3.2–3) равен орбитальному квантовому числу .

Второй корень равен сумме , взятой со знаком минус или иначе равен отрицательному значению квантового числа Зоммерфельда.

Значения и даны в восьмой и девятой строках Таблицы.

Отметим аналогичное наличие двух корней при рассмотрении нами полного углового момента и спинового углового момента электрона.

В десятой строке дана разность квадратов моментов, обозначенная как :

Здесь квадрат орбитального углового момента также представлен как разность квадратов моментов, что сходно с выражением (3.2-2).

Отметим, что все значения моментов и их квадратов в таблице (кроме пятой строки) целочислены, и в этом смысле их можно назвать квантованными.

3. На Рисунке 3.2.1 для значения азимутального квантового числа дано построение, иллюстрирующее данные Таблицы 3.2.1.

Выделенным направлением является ось Z, что может быть обусловлено, например, слабым магнитным полем Земли.

Покажем получение выражения (3.2-1) для и положительного направления оси Z.

На рисунке 3.2.1 из точки 0 радиусом проведена окружность, а также дуга в первой четверти окружности радиусом согласно пятой строки таблицы.

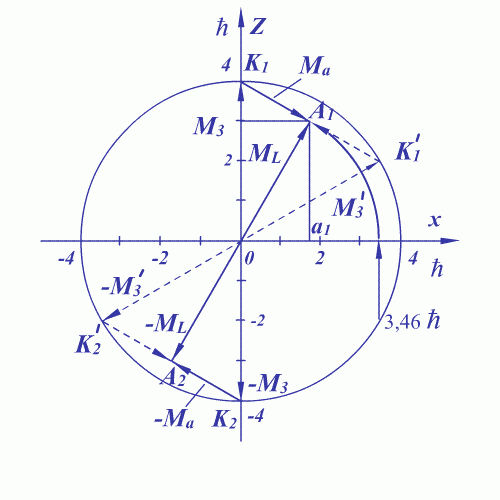
Рис. 3.2.1. Орбитальный угловой момент электрона и его связь с моментом количества движения . Азимутальное квантовое число .

Для определения точки найдем пересечение дуги радиусом с прямой линией, определяемой значением .

Прямой угол при точке образован вектором и вектором . Вектор есть гипотенуза прямоугольного треугольника .

Таким образом, рассматривая треугольник , для положительного направления оси Z получим искомое выражение (3.2-1),:

На Рисунке дан пунктиром треугольник , для моментов которого также справедливо выражение (3.2–1). При этом можно предположить, что вектор орбитального углового момента электрона равен среднему арифметическому значению векторов и , т.е.

Из рисунка 3.2.1 и выражения (3.2-12) можно сделать следующее заключение.
Орбитальный угловой момент электрона Ланде в действительности может являться средним арифметическим векторов и _,которые описывают орбитальный момент электрона в теории Бора – Зоммерфельда.

По мере уменьшения азимутального квантового числа: значения уменьшается последовательно как: 3,46; 1,41; 0. При этом угол между векторами и также последовательно увеличивается следующим образом: 60^о, 90^о , 180^о; т.е. в последнем случае векторы и направлены противоположно друг другу и поэтому здесь угловой момент электрона равен нулю, что соответствует выражению

Сделаем выводы относительно орбитального углового момента.

имеет «семейство» квантовых чисел, содержащее две величины:

Обе величины удовлетворяют значениям квадрата орбитального момента электрона, т.е.:

– Показана связь орбитального углового момента Ланде с моментом количества движения электрона теории Бора – Зоммерфельда через выражения (3.2–2) и (3.2–9).

Считается, что различие между формулой Ланде (3.1–1) и Зомерфельда (3.1–2) обусловлено неправильностью классического подхода Зоммерфельда. Используя векторные диаграммы для анализа угловых моментов, нами показано, что угловой момент по формуле Ланде возможно является средним арифметическим моментов формулы Зоммерфельда.

Приведем кратко результаты, полученные в третьей части нашей работы:

– показано наличие «семейства» квантовых чисел из двух величин, которые удовлетворяют

квадратам орбитального, полного и спинового моментам электрона,

– показана связь указанных моментов с орбитальным моментом электрона

– показано влияние спинового момента ядра на ориентировку, в частности,

В связи с новизной подхода к рассмотрению угловых моментов электрона на основе классической физики, полученные результаты оцениваются как первое приближение.

Результаты этой работы могут привлечь внимание работающих в области атомной физики, исследователей, студентов, а также заинтересованных читателей.

Шидловский Александр Игнатьевич

ATOM ВОДОРОДА – САМЫЙ ПРОСТОЙ ИЗ АТОМОВ

Продолжение теории Нильса Бора

Продолжение теории Нильса Бора. М.: Вестник, 2000 г. С . 63.

Цена книги 40 рублей.