
Новые публикации: "Частота излучения фотона совпадает со средней частотой излучения электрона в переходе." >>>
Шидловский Александр Игнатьевич
ATOM ВОДОРОДА - САМЫЙ ПРОСТОЙ ИЗ АТОМОВ
Продолжение теории Нильса Бора
Книга 2
2. ПЕРЕХОДЫ ЭЛЕКТРОНА С ПОТЕРЕЙ
ОРБИТАЛЬНОГО МОМЕНТА В ЛИНИЯХ
СЕРИИ БАЛЬМЕРА
Представлена интернет-версия (сокращенный вариант) Книги 2
2.1
Потеря энергии в переходах 4d2p, 5d2p, … nd2p
2.2
Потеря момента количества движения
2.3
Общие результаты
Рассмотрены переходы, приводящие к образованию линий серии Бальмера. Здесь излучательные переходы электрона происходят между стационарными эллиптическими и круговой орбитами. В течение перехода электрон движется вокруг ядра по эллиптическим, спирально уменьшающимся орбитам, а его орбитальный момент уменьшается на постоянную Планка ħ.
2.1. ПОТЕРЯ ЭНЕРГИИ В ПЕРЕХОДЕ
В этой части нашей работы рассмотрены переходы: 4d2p, 5d2p, … nd2p [2.1.1].
Они показаны на Рисунке 2.1.1, где по оси ординат слева дана энергия Е электрона в электрон-вольт (эВ). По оси ординат справа дано «относительное» значение энергии электрона:
![]() .
.
n – номер круговой стационарной орбиты или энергетического
состояния электрона, а также главное квантовое число,
![]() –
большая полуось текущей эллиптической орбиты.
–
большая полуось текущей эллиптической орбиты.
По оси абсцисс (дана
сверху) приведены значения азимутального квантового числа ![]() Зоммерфельда и орбитального
квантового числа
Зоммерфельда и орбитального
квантового числа ![]() Ланде.
Ланде.
В n-ом энергетическом состоянии (на n-ой стационарной эллиптической орбите) электрон обладает энергией:
![]()
![]() – относительное значение большой полуоси
эллиптической
– относительное значение большой полуоси
эллиптической
стационарной орбиты
![]()
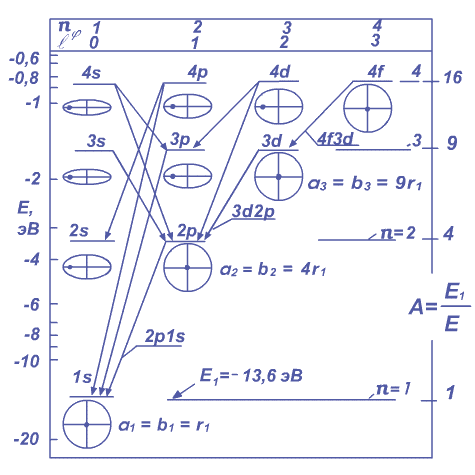
Рис. 2.1.1. Упрощенная схема энергетических уровней и излучательных переходов электрона в атоме водорода. Эллиптические и круговые орбиты электрона показаны иллюстративно, ядро дано в виде точки. Большие полуоси эллиптических орбит условно даны одного размера.
Покажем процесс постепенной потери энергии электроном в nd2p переходе [2.1.2]. Отнесем выражение (2.1 – 2) к текущему энергетическому состоянию электрона в течение перехода
![]()
![]() –
относительное значение большой полуоси текущей
–
относительное значение большой полуоси текущей
эллиптической орбиты.
Дифференцируя (2.1 – 4), получим потерю энергии dE электроном при уменьшении относительного значения большой полуоси на dA:
![]()
Интегрируя (2.1–5) с учетом (2.1–2), получим количество энергии, постепенно теряемое электроном в nd2p переходе и уносимое с излучением фотона,
здесь n ≥ 3 :
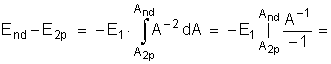
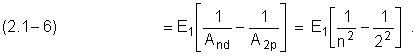
Количество энергии, теряемое электроном в процессе перехода, совпадает с полученным на основе закона сохранения энергии.
Теперь процесс перехода предстает как постепенная потеря энергии электроном в зависимости от уменьшения относительного значения большой полуоси эллиптической орбиты А или от уменьшения главного квантового числа n.
2.1.1) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть 2. М.: УРСС, 1998. С. 13-78.
2.1.2) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть 2. М.: УРСС, 1998. С. 20-23.
2.2. ПОТЕРЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
Рассмотрим процесс потери момента количества движения электроном в nd2p переходе.
Запишем выражение для текущего момента количества движения электрона, вращающегося вокруг ядра по эллиптической орбите [2.2.1]:
![]()
b, E – текущие значения малой полуоси эллиптической орбиты и энергии
электрона (по абсолютной величине) в процессе перехода,
m – масса электрона.
Перепишем (2.2–1), используя (2.1–2)
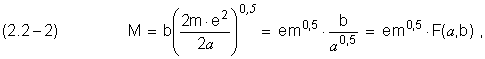
т.е. текущий момент количества движения
электрона является функцией двух переменных: F( ![]() , b).
, b).
Запишем (2.2–2) с учетом (2.1–1)
и выражения теории Бора
![]() [2.2.2] :
[2.2.2] :
![]()
![]()
В – относительная величина малой полуоси эллиптической орбиты электрона.
![]()
Следовательно:
![]()
Таким
образом, текущее значение азимутального квантового числа ![]() равно отношению
относительных значений малой полуоси В и большой полуоси А в степени одна
вторая. С другой стороны, текущее значение
равно отношению
относительных значений малой полуоси В и большой полуоси А в степени одна
вторая. С другой стороны, текущее значение ![]() равняется
относительному значению момента количества движения электрона.
равняется
относительному значению момента количества движения электрона.
Рассмотрим потерю момента количества движения электроном, например в 4d2p переходе, который обусловливает образование второй линии серии Бальмера.
Запишем полный дифференциал функции
F( ![]() , b) выражения (2.2–2):
, b) выражения (2.2–2):
![]()
Интегрируя (2.2.–6), получим потерю момента количества движения электроном в переходе:
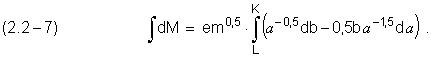
К, L – точки начала и конца перехода (или начальный и конечный энергетические уровни).
На Рисунке 2.2.1 нанесена
начальная точка ![]() и конечная точка
и конечная точка ![]() ,
между которыми проходит «траектория» 4d2p перехода электрона.
,
между которыми проходит «траектория» 4d2p перехода электрона.
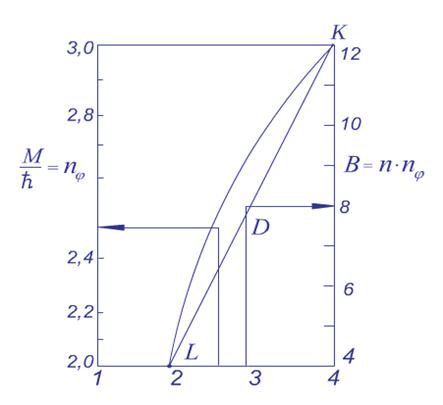
По оси ординат (справа) даны относительные значения малой полуоси В, а по оси абсцисс даны относительные значения большой полуоси А в степени одна вторая.
Значение момента количества движения, теряемого электроном в переходе, не зависит от вида «траектории» [2.2.3] .
В дальнейшем в качестве «траектории» изменения переменных А0,5 и В принята прямая линия, которая нанесена на Рисунке 2.2.1 между точками К и L.
![]()
Рисунок 2.2-1. Изменение относительных значений полуосей
( В и ![]() )
)
текущей эллиптической орбиты электрона в процессе 4d2p перехода.
Параметры точек К, D и L этой прямой возьмем из Таблицы 2.2.1.
Таблица 2.2.1.
| Обозначение точки |
Параметры точки (переход 4d2p) |
| K (начальная) |
|
| D (промежуточная) |
|
| L (конечная) |
|
Таким образом, прямая KL, включая и промежуточную точку D, отражает собой изменение полуосей эллиптической орбиты электрона в течение 4d2p перехода.
Запишем «траекторию» изменения переменных А0,5 и В в течение 4d2p перехода как уравнение прямой линии, показанной на Рисунке 2.2.1.
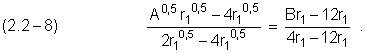
Упростим (2.2 – 8):
![]()
![]()
Используя (2.2–4), (2.2–10), запишем:
![]()
С учетом (2.1–1) получим:
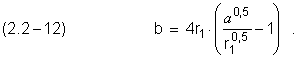
![]()
Подставим эти значения в (2.2 – 7) и получим:
![]()
![]()
![]()
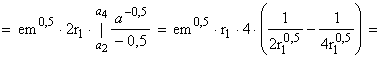
![]()
Напомним:
![]()
![]() и
и
![]() .
.
Таким образом, потеря момента количества движения в 4d2p переходе составит:
![]()
.
т.е. момент количества движения, постепенно теряемый электроном в процессе 4d2p перехода (и постепенно уносимый фотоном), оказывается равным постоянной Планка ħ.
Важное значение результата (2.2–18) состоит в том, что постоянная Планка ħ получает простой физический смысл. Она равна интегралу (сумме) потерь текущего момента количества движения электрона в процессе его 4d2p перехода по спирально уменьшающимся эллиптическим орбитам.
Отметим следующее. Момент количества движения, теряемый электроном, выражается через постоянную Планка ħ. Это указывает на возможность применения классической физики для описания явлений микромира.
Описание процесса потери момента количества движения электроном в nd2p переходе несколько трудоемко. Однако все преобразования доступны студенту технического института.
2.2.1) Ландау Л. Д., Лившиц Е.М. Механика.
М.: Наука, 1965. С. 8.
2.2.2) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть вторая. М.: УРСС, 1998. С. 27.
2.2.3) Шидловский А.И. Атом водорода – самый простой из атомов.
Часть вторая. М.: УРСС, 1998. С. 29.
Приведем кратко другие результаты, полученные нами во второй части нашей работы.
Для электрона в переходе по спирально уменьшающимся эллиптическим орбитам определены:
– переносная, радиальная и общая скорость;
– переносное, радиальное и общее ускорение;
– кинетическая, потенциальная и полная энергия;
– интенсивность излучения энергии;
– число оборотов электрона в переходе и время перехода.
Для рассмотренных nd2p переходов, приводящих к образованию линий серии Бальмера, полученные результаты подтверждают наше предположение об эллиптическом характере движения электрона в переходе между стационарными эллиптическими и круговой орбитами в атоме водорода.
Таким образом, на основе классической физики для атома водорода Бора – Зоммерфельда рассмотрены задачи, постановка которых обычно невозможна в квантовой механике.
При этом используется наглядная модель движения электрона и применяется простая математика.
Наша работа может привлечь внимание специалистов атомной физики, исследователей, студентов, заинтересованных читателей.
Подробно данный материал изложен в книге
Шидловский А.И. Атом водорода - самый простой из атомов. Книга 2.
Продолжение теории Нильса Бора. М.: УРСС, 1998 г. 78 С.
Цена
книги 40 рублей
Автор с признательностью примет замечания и предложения
по адресу: 127576, Москва, ул. Череповецкая, д. 14, кв. 168,
по телефону: 8(499) 200-94-28,
по эл. почте: E-mail:Shidlowsky@gmail.com Шидловскому Александру Игнатьевичу.
По вопросу приобретения опубликованных книг можно обратиться по указанному здесь адресу.
Использование материалов сайта допускается только с письменного разрешения автора.