
Новые публикации: "Частота излучения фотона совпадает со средней частотой излучения электрона в переходе." >>>
Шидловский Александр Игнатьевич
кандидат технических наук
ATOM ВОДОРОДА - САМЫЙ ПРОСТОЙ ИЗ АТОМОВ
Продолжение теории Нильса Бора
Книга 1
1. ИЗЛУЧАТЕЛЬНЫЙ ПЕРЕХОД ЭЛЕКТРОНА
В АТОМЕ ВОДОРОДА БОРА
Представлена интернет-версия (сокращенный вариант) Книги 1
1.1
Потеря энергии в переходе
1.2 Потеря
момента количества движения
1.3
Время перехода электрона
1.4
Общие результаты
1.1. ПОТЕРЯ ЭНЕРГИИ В ПЕРЕХОДЕ
Рассмотрены излучательные переходы электрона между соседними круговыми стационарными орбитами в атоме водорода.
В процессе такого перехода движение электрона вокруг ядра происходит по круговым, спирально уменьшающимся орбитам. [1.1.1]. Это переходы 2p1s, 3d2p, 4f3d, ... и т.д. Они показаны на Рисунке 1.1.1, где по оси ординат слева дана энергия Е электрона в электрон-вольт (эВ). По оси ординат справа дано «относительное» значение энергии электрона:
![]()
n – номер круговой стационарной орбиты, или энергетического состояния
электрона, а также главное квантовое число,
![]() – большая полуось текущей эллиптической
орбиты.
– большая полуось текущей эллиптической
орбиты.
Покажем потерю энергии электроном в переходе на основе закона сохранения энергии, как это сделал Бор в 1913 году.
В n-ом энергетическом состоянии или на n-ой круговой стационарной орбите электрон обладает энергией
![]()
е – заряд электрона,
![]() – радиус n-ой круговой стационарной орбиты
электрона,
– радиус n-ой круговой стационарной орбиты
электрона,
![]() – энергия электрона, находящегося
на первой круговой стационарной
– энергия электрона, находящегося
на первой круговой стационарной
орбите с радиусом ![]() .
.
Перейдя на (n –1)-ую круговую стационарную орбиту, более близкую к ядру, электрон станет обладать энергией
![]()
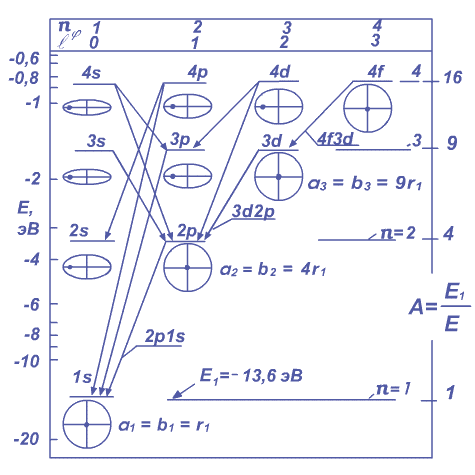
Рисунок 1.1.1.
Упрощенная схема энергетических уровней и излучательных переходов электрона в атоме водорода. Сверху по оси абсцисс приведены
значения азимутального квантового числа ![]() Зоммерфельда и орбитального квантового числа
Зоммерфельда и орбитального квантового числа ![]() Ланде. Эллиптические
и круговые орбиты электрона показаны иллюстративно, ядро дано в виде
точки. Большие полуоси эллиптических орбит условно даны одного размера.
Ланде. Эллиптические
и круговые орбиты электрона показаны иллюстративно, ядро дано в виде
точки. Большие полуоси эллиптических орбит условно даны одного размера.
Потеря энергии электроном в переходе составит
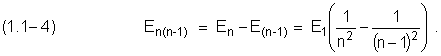
В выражении (1.1– 4) закон сохранении энергии регистрирует потерю энергии электроном. Однако, закономерности самого процесса потери энергии не отражаются. Переход представляется как «перескок» электрона из n – ого в ( n – l ) – oe энергетическое состояние.
Рассмотрим процесс потери энергии электроном в переходе между соседними круговыми стационарными орбитами. В начале перехода, когда электрон начинает спонтанно сходить с круговой стационарной орбиты, он оказывается под действием закона электродинамики, который, в частности, сводится к следующему.
Обращение электрически заряженного электрона по круговой траектории есть криволинейное движение с ускорением, и поэтому электрон должен терять энергию путем испускания электромагнитного излучения.
Теряя энергию, электрон движется по спирально уменьшающейся окружности вокруг ядра атома водорода.
Потеря энергии электроном связана с изменением радиуса r спиральной орбиты соотношением
![]()
Это соотношение получается при дифференцировании выражения (1.1–2), но отнесенного к текущему значению энергии Е электрона.
В течение всего перехода с n-ой круговой стационарной орбиты
с радиусом ![]() на соседнюю (n – 1)-ую круговую стационарную орбиту с радиусом
на соседнюю (n – 1)-ую круговую стационарную орбиту с радиусом ![]() электроном теряется, а фотоном соответственно уносится
энергия.
электроном теряется, а фотоном соответственно уносится
энергия.
Интегрируя (1.1–5), получим энергию, теряемую электроном в переходе
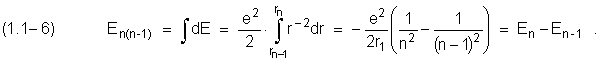
Количество энергии, теряемое электроном в процессе перехода, совпадает с выражением (1.1–4), полученным при использовании закона сохранения энергии. Теперь переход электрона между соседними круговыми стационарными орбитами представляется как процесс постепенной потери его энергии, а не как «перескок» между энергетическими уровнями.
Движение электрона в переходе определяется законами сохранения энергии, механики и Кулона. Поэтому в отсутствие внешних воздействий в движении электрона по круговым, спиральным орбитам должен отсутствовать элемент случайности.
1.1.1) Шидловский А.И. Атом водорода - самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 57-61.
1.2. ПОТЕРЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
Рассмотрим процесс постепенной потери момента количества движения М электроном при его переходе между соседними, круговыми стационарными орбитами. Отметим, что квантовая механика подходит к этому только на основе закона сохранения момента, т.е. не рассматривает сам процесс потери орбитального момента электрона в течение перехода.
![]()
v, r – текущие значения скорости электрона и радиуса орбиты,
m – масса электрона.
Используем для случая текущей круговой орбиты электрона, известную формулу теории атома водорода Бора [1.2.1] :
![]()
Подставим выражение (1.2–2) для скорости v электрона в (1.2–1):
![]()
Дифференцируя (1.2–3), получим зависимость потери момента dM электрона от уменьшения радиуса орбиты на dr :
![]()
В процессе перехода с круговой
стационарной орбиты, радиусом ![]() , на соседнюю круговую стационарную
орбиту, радиусом
, на соседнюю круговую стационарную
орбиту, радиусом ![]() , электроном теряется, а фотоном уносится момент количества движения:
, электроном теряется, а фотоном уносится момент количества движения:
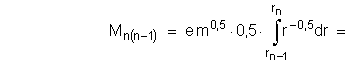
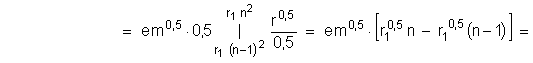
![]()
При упрощении (1.2–5) использовано
выражение (1.2–2) для первого
стационарного состояния атома водорода, где скорость электрона и радиус
его орбиты составляют: ![]() и
и ![]() , т.е. применено выражение теории Бора [1.2.1] :
, т.е. применено выражение теории Бора [1.2.1] :
![]()
Таким образом, момент количества движения, постепенно теряемый электроном в переходе, и момент, уносимый фотоном, оказываются равными постоянной Планка ħ, что согласуется с результатом, получаемым при использовании закона сохранения момента. Теперь виден процесс постепенной потери момента количества движения по мере уменьшения радиуса орбиты электрона в течение перехода.
Важный результат состоит в том, что согласно (1.2-5) постоянная Планка ħ приобретает наглядный физический смысл. Она оказывается равной интегралу (сумме) потерь текущего момента количества движения электрона в процессе его перехода между круговыми стационарными орбитами.
1.2.1) Шидловский А.И. Атом водорода - самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 16.
В квантовой теории, говорит Бор: «совершенно не рассматривается время, в течении которого происходят переходы» [1.3.1], а «… вопрос о промежутке времени, в течение которого происходит излучение, связанное с переходом, вызывает большие трудности» [1.3.2] .
Определим время перехода электрона между соседними, круговыми стационарными орбитами на основе классической физики.
Итенсивность излучения энергии согласно электродинамике запишем как текущую скорость потери энергии электроном в процессе его перехода между соседними круговыми стационарными орбитами:
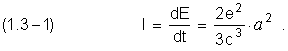
с – скорость света.
Получим выражение для ускорения электрона на текущей круговой орбите, используя (1.2–2):
![]()
Найдем соотношение ![]() , используя (1.1–5):
, используя (1.1–5):
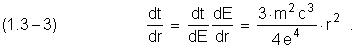
Интегрируя (1.3–3) и применяя
(1.2–2), определим время перехода электрона между соседними круговыми
стационарными орбитами; при этом ![]() ,
, ![]() .
.
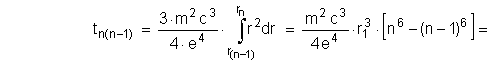
![]()
![]()
Здесь ![]() постоянная тонкой структуры:
постоянная тонкой структуры:
![]()
Период обращения электрона по первой, круговой стационарной орбите:
![]()
Относительное значение большой полуоси орбиты
![]()
Условное число оборотов электрона
на первой,
круговой стационарной орбите при потере им энергии ![]() с «интенсивностью»
с «интенсивностью» ![]() [1.3.4]
:
[1.3.4]
:
![]()
Условное
время потери энергии ![]() электроном с интенсивностью
электроном с интенсивностью ![]() на первой,
круговой стационарной орбите
на первой,
круговой стационарной орбите
![]()
Для рассматриваемого случая спиральных круговых орбит в переходе относительное значение большой полуоси орбиты :
![]()
Относительное значение радиуса R орбиты электрона :
![]()
В Таблице 1.3.1 сопоставлено время перехода ![]() электрона, вычисленное в данной работе, с временем жизни перехода
электрона, вычисленное в данной работе, с временем жизни перехода ![]() по данным квантовой механики.
по данным квантовой механики.
Первая строка Таблицы 1.3.1. отражает формально
«1sp» переход электрона с первой, стационарной орбиты, где n =1, на ядро – протон, где ![]() .
.
Остальные пять переходов соответствуют первым линиям в серии Лаймана, Бальмера, Пашена, Брэкета и Пфунда.
Во втором столбце Таблицы 1.3.1. приведена вероятность W перехода электрона по данным квантовой механики [1.3.5].
В третьем столбце дано время жизни перехода
![]()
В четвертом столбце дано округленное значение времени перехода, подсчитанное по (1.3 – 4) .
Таблица 1.3.1.
| Переход |
Вероятность перехода
|
Время жизни перехода
|
Время перехода по (1.3-4)
|
Отношение времен
|
| 1 |
2 |
3 |
4 |
5 |
| «1sp» 2p1s 3d2p 4 f 3d 5g4 f 6h5g |
– 6,26 · 10 8 6,46 · 10 7 1,38 · 10 7 4,25 · 10 6 1,64 · 10 6 |
– 0,16 · 10 – 8 1,55 · 10 – 8 7,25 · 10 – 8 23,5 · 10 – 8 61,0 · 10 – 8 |
1,55 · 10 –11 0,98 · 10 – 9 1,04 · 10 – 8 5,24 · 10 – 8 18,0 · 10 – 8 48,3 · 10 – 8 |
– 1,63 1,49 1,38 1,31 1,26 |
Как видно из 5-го столбца Таблицы 1.3.1, расхождение между временем жизни перехода ![]() и временем перехода
и временем перехода ![]() электрона сравнительно
невелико, носит систематический характер, монотонно уменьшаясь с ростом
номера перехода.
электрона сравнительно
невелико, носит систематический характер, монотонно уменьшаясь с ростом
номера перехода.
Отметим следующее.
Сопоставляемые в Таблице 1.3.1.
величины ![]() и
и ![]() имеют не вполне одинаковый физический
смысл.
имеют не вполне одинаковый физический
смысл.
В квантовой механике излучательное
время жизни перехода ![]() определяется как время, за которое
число атомов возбужденного состояния уменьшается
определяется как время, за которое
число атомов возбужденного состояния уменьшается
в 2,72 раза.
В данной работе ![]() – время перехода электрона между стационарными
состояниями (круговыми стационарными
орбитами). При этом в течение времени
– время перехода электрона между стационарными
состояниями (круговыми стационарными
орбитами). При этом в течение времени ![]() электрон непрерывно испускает энергию.
электрон непрерывно испускает энергию.
Таким образом, время ![]() равно также времени излучения фотона,
равно также времени излучения фотона, ![]() .
.
Фотон можно представить волновым образованием.
Например, в случае 3d2p перехода временная продолжительность фотона, согласно Таблице 1.3.1., составляет
![]()
а его линейная пространственная протяженность
![]()
![]() .
.
С – скорость света.
1.3.1) Нильс Бор. Избранные научные труды.
Т. 2. М.: Наука, 1971. С. 24.
1.3.2) Нильс Бор. Избранные научные труды.
Т. 1. М.: Наука, 1970. С. 530.
1.3.3) Шидловский А.И. Атом водорода - самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 32.
1.3.4) Шидловский А.И. Атом водорода - самый простой из атомов.
Минск: ВЭВЭР, 1997. С. 100.
1.3.5) Собельман И. И. Введение в теорию атомных спектров
М.: Наука, 1977. С. 295.
Приведем кратко другие результаты, полученные при определении характеристик излучательного перехода электрона в атоме водорода Бора:
– показано, что электрон испускает энергию с интенсивностью, которую
требует электродинамика,
– определено число оборотов электрона вокруг ядра,
– определена средняя частота излучения фотона, которая сопоставлена
с теоретической частотой,
– получена модифицированная формула Эйнштейна для случая потери
энергии электроном в переходе.
Результаты выражений (1.1–6) и (1.2–5) подтверждают, в частности, сделанное нами предположение о круговом характере движения электрона по спирально уменьшающимся орбитам в рассмотренных переходах атома водорода.
Таким образом, на основе классической физики для атома водорода рассмотрены задачи, постановка которых до сих пор невозможна в квантовой механике.
При этом использована наглядная модель движения электрона и применена простая математика.
Наша работа может привлечь внимание
специалистов атомной физики, исследователей, студентов, заинтересованных
читателей.
Подробно данный материал изложен в книге:
Шидловский А.И. Атом водорода - самый простой из атомов. Книга 1.
Продолжение теории Нильса Бора. Минск: ВЭВЭР, 1997. 127 С.
Цена книги 50 рублей.
Автор с признательностью примет замечания и предложения
по адресу: 127576, Москва, ул. Череповецкая, д. 14, кв. 168,
по телефону: 8 (499) 200-94-28,
по эл. почте: E-mail:Shidlowsky@gmail.com
Шидловскому Александру Игнатьевичу.
По вопросу приобретения книг можно обратиться по указанному здесь адресу.
Использование материалов сайта допускается только с письменного разрешения автора.